ちょうど部屋を片していると、

散乱している中に数学Cの参考書がぽつり。

パラパラめくると昔はあったはずの「行列」の単元が無い。

おや？と思って文科省の学習指導要領HPを見ました。

「膨大な学習が必要な高校数学は単元習得に割く時間が限られ、

知っているほうが良いが興味・余力がある場合に習得する内容になっている」と。

なるほど。ちらりとその例示（以下一部変更抜粋）。

インターネットは，情報社会において重要な位置を占めている。中でも検索エンジンはインターネットの中心的なツールであり，検索窓と呼ばれるボックスに「検索キーワード」を入力すると， キーワードを含むウェブページ（サイト）を「重要なものを上位にして」瞬時にリストアップする機能を持つ。この機能の背景には，進んだ行列の理論と，点と線からなる図形である「グラフ」の理論がある。

例）各ウェブページに，次の条件をみたすように点数をつける。 

(1) すべてのページに渡る点数の和は1とする。

(2) 自分のページから他のページにリンクがあるとき，自分の点数をそれに等分配する。

(3) 自分のページの点数は，他のページから等分配された総点数と一致する。

条件 (3) により，多くのページからリンクされているページの点数の値は大きくなり，さらに，点数が上位のページからリンクされているページの点数の値は大きくなることから，この点数付けは重要なウェブページを上位にするという要請を満たしている。

インターネットにおけるウェブページを点，1つのウェブページ A から他のウェブページ B にリンクが張られていれば，A から B に向かう矢印（ベクトル）で表す。ウェブページの数を 4 とし，それらに番号①，②，③，④ を与える。そして，それぞれに配分される点数を x1， x2， x3， x4 とする（図1）。

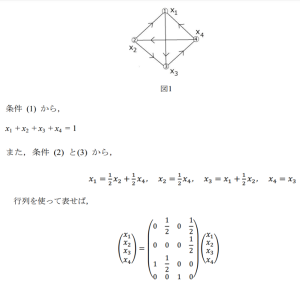
注目すべきは，行列の各列の成分の和が1に等しいこと，および同じ列には0を除けば同じ数が並んでいること。これは，各ウェブページからの点数が等配分されることに対応する。 こうして得られる連立方程式を解けば，𝑥1= 3/13，  𝑥2= 2/13，  𝑥3= 4/13，  𝑥4= 4/13  となって，ウェブページ③と④が高得点となることがわかる。

これは，一般にウェブページの数を n とするとき，すべての成分が 0 以上，かつ各列の成分の和が 1であるような n 次の正方行列 P を用いることにより，問題は Px = x のベクトル解 x（ただし，成分はすべて 0 以上）を求めることに帰着される。（文部科学省　学習指導要領「生きる力」(授業改善のための参考資料（教職員向け） 高等学校数学科教材（行列入門）より)）

当時は数Cには高校レベルの内容でベクトルと行列もあったけど、

実務ではこんな感じで対応して使っていることなのか～と改めて教えてもらいました。

ついでに最近、偶然にも耳にした高校時代の数学教師Tの顔も浮かんできました（S高校校長retireして元気かな笑）。

目に見えない理論背景が今の実生活の一部になっている。

振り返ってみると自分のしていることは誰かの役に立っているのかな。

方向性のきちんとしたベクトルと行列で量も十分なように。

実生活を充実させるために、エビデンスもナラティブも含めてきちんとした仕事になっているのかな。

想像を絶するくらいの曲がってしまった環境をただしい位置ベクトルにもどさないと。

そうしないといまの自分の存在意義が無く、無力感に苛まれるようになってしまう。

とんでもない現実も、もう少し深く洞察・追求すれば、いろんなことがつながるかもしれない。

真面目に取り組んだものが、ベクトルが行も列も引っさげて正しい方向へ向かわせるかもしれない。